Toward a quantum computer that calculates molecular energy
Developed by Columbia chemistry professor David Reichman and postdoc Joonho Lee with researchers at Google Quantum AI, the algorithm uses up to 16 qubits on Sycamore, Google's 53-qubit computer, to calculate ground state energy, the lowest energy state of a molecule. "These are the largest quantum chemistry calculations that have ever been done on a real quantum device," Reichman said.
The ability to accurately calculate ground state energy, will enable chemists to develop new materials, said Lee, who is also a visiting researcher at Google Quantum AI. The algorithm could be used to design materials to speed up nitrogen fixation for farming and hydrolysis for making clean energy, among other sustainability goals, he said.
The algorithm uses a quantum Monte Carlo, a system of methods for calculating probabilities when there are a large number of random, unknown variables at play, like in a game of roulette. Here, the researchers used their algorithm to determine the ground state energy of three molecules: heliocide (H4), using eight qubits for the calculation; molecular nitrogen (N2), using 12 qubits; and solid diamond, using 16 qubits.
Ground state energy is influenced by variables such as the number of electrons in a molecule, the direction in which they spin, and the paths they take as they orbit a nucleus. This electronic energy is encoded in the Schrodinger equation. Solving the equation on a classical computer becomes exponentially harder as molecules get bigger, although methods for estimating the solution have made the process easier. How quantum computers might circumvent the exponential scaling problem has been an open question in the field.
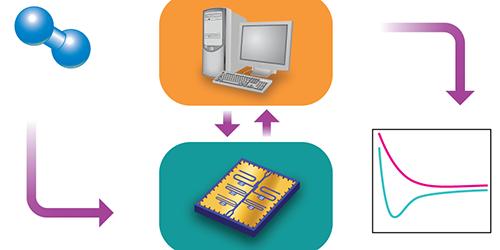
In principle, quantum computers should be able to handle exponentially larger and more complex calculations, like those needed to solve the Schrodinger equation, because the qubits that make them up take advantage of quantum states. Unlike binary digits, or bits, made up of ones and zeros, qubits can exist in two states simultaneously. Qubits, however, are fragile and error-prone: the more qubits used, the less accurate the final answer. Lee's algorithm harnesses the combined power of classical and quantum computers to solve chemistry equations more efficiently while minimizing the quantum computer's mistakes.
"It's the best of both worlds," Lee said. "We leveraged tools that we already had as well as tools that are considered state-of-the-art in quantum information science to refine quantum computational chemistry."
A classical computer can handle most of Lee's quantum Monte Carlo simulation. Sycamore jumps in for the last, most computationally complex step: the calculation of the overlap between a trial wave function -- a guess at the mathematical description of the ground state energy that can be implemented by the quantum computer -- and a sample wave function, which is part of the Monte Carlo's statistical process. This overlap provides a set of constraints, known as the boundary condition, to the Monte Carlo sampling, which ensures the statistical efficiency of the calculation.
The prior record for solving ground state energy used 12 qubits and a method called the variational quantum eigensolver, or VQE. But VQE ignored the effects of interacting electrons, an important variable in calculating ground state energy that Lee's quantum Monte Carlo algorithm now includes. Adding virtual correlation techniques from classic computers could help chemists tackle even larger molecules, Lee said.
The hybrid classical-quantum calculations in this new work were found to be as accurate as some of the best classical methods. This suggests that problems could be solved more accurately and/or quickly with a quantum computer than without -- a key milestone for quantum computing. Lee and his colleagues will continue to tweak their algorithm to make it more efficient, while engineers work to build better quantum hardware.
"The feasibility of solving larger and more challenging chemical problems will only increase with time," Lee said. "This gives us hope that quantum technologies that are being developed will be practically useful."