Entanglement unlocks scaling for quantum machine learning

"Our work proves that both big data and big entanglement are valuable in quantum machine learning. Even better, entanglement leads to scalability, which solves the roadblock of exponentially increasing the size of the data in order to learn it," said Andrew Sornborger, a computer scientist at Los Alamos and a coauthor of the paper published Feb. 18 in Physical Review Letters. "The theorem gives us hope that quantum neural networks are on track towards the goal of quantum speed-up, where eventually they will outperform their counterparts on classical computers."

The classical No-Free-Lunch theorem states that any machine-learning algorithm is as good as, but no better than, any other when their performance is averaged over all possible functions connecting the data to their labels. A direct consequence of this theorem that showcases the power of data in classical machine learning is that the more data one has, the better the average performance. Thus, data is the currency in machine learning that ultimately limits performance.

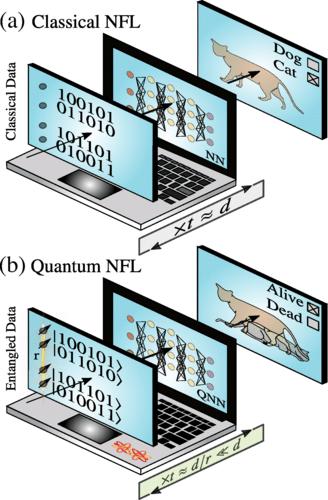
The new Los Alamos No-Free-Lunch theorem shows that in the quantum regime entanglement is also a currency, and one that can be exchanged for data to reduce data requirements.

Using a Rigetti quantum computer, the team entangled the quantum data set with a reference system to verify the new theorem.

"We demonstrated on quantum hardware that we could effectively violate the standard No-Free-Lunch theorem using entanglement, while our new formulation of the theorem held up under experimental test," said Kunal Sharma, the first author on the article.

"Our theorem suggests that entanglement should be considered a valuable resource in quantum machine learning, along with big data," said Patrick Coles, a physicist at Los Alamos and senior author on the article. "Classical neural networks depend only on big data."

Entanglement describes the state of a system of atomic-scale particles that cannot be fully described independently or individually. Entanglement is a key component of quantum computing.